Подготовка к ОГЭ и ЕГЭ - решение заданий и теория
На oge-ege.info, мы предлагаем всестороннюю поддержку для учащихся, готовящихся к ОГЭ и ЕГЭ. Наша миссия - обеспечить вас всеми необходимыми знаниями для успешной сдачи экзаменов.
📚 Что мы предлагаем:
- База заданий: большая коллекция заданий ОГЭ и ЕГЭ с подробными решениями и пояснениями.
- Видеоуроки: наши эксперты предлагают обучающие видео для более глубокого понимания сложных тем.
- Теория и формулы: для безошибочного продвижения вперед.
💡 Почему выбирают нас:
- Актуальность материалов: мы регулярно обновляем нашу базу заданий, чтобы она соответствовала последним требованиям экзаменов.
- Доступность: получите доступ к учебным материалам в любое время, из любой точки мира.
- Пошаговое объяснение решений: все решения подробно объясняются.
🔍 Начните свою подготовку сегодня:
- Изучайте материалы и решайте задания.
- Смотрите видеоуроки и разборы заданий.
📢 Присоединяйтесь к oge-ege.info и сделайте свой путь к успешной сдаче ОГЭ и ЕГЭ проще и эффективнее!
Интересные задания ОГЭ и ЕГЭ (ФИПИ) и их решение
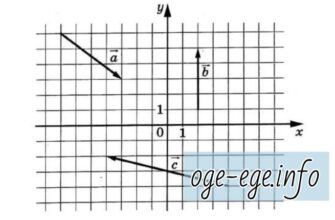
На координатной плоскости изображены векторы , и . Найдите длину вектора . Решение Найдем координаты вектора, для этого найдем координаты

Задача. В коробке 6 синих, 12 красных и 7 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что
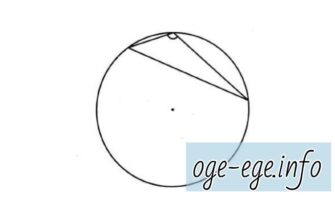
Задача. Радиус окружности равен . Найдите величину тупого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.
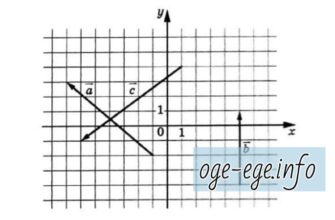
Задача. На координатной плоскости изображены векторы , и . Найдите скалярное произведение . Решение Найдем координаты точек начала и конца
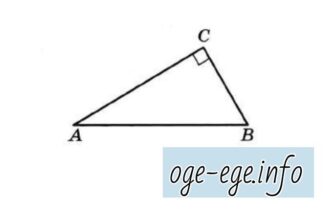
В треугольнике ABC угол С равен 90°, , . Найдите . Решение Запишем соотношение сторон и углов в треугольнике: Чтобы найти AC нам надо знать AB.
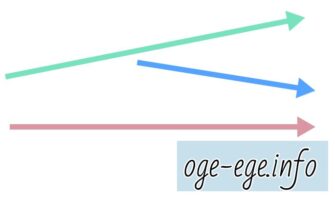
Задача. Даны векторы и . Известно, что векторы и сонаправленные, а . Найдите . Решение Для решения этой задачи нужно учесть два условия
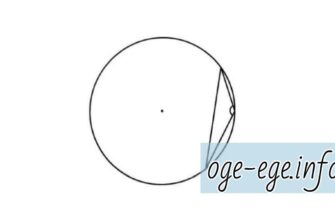
Задача. Найдите хорду, на которую опирается угол 135º, вписанный в окружность радиуса 3\/2. Решение Сделаем рисунок к задаче.
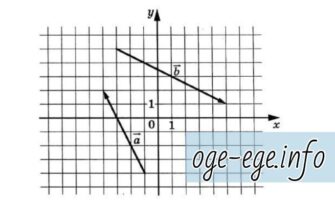
Задача. На координатной плоскости изображены векторы и . Найдите , где — угол между векторами и . Решение Для нахождения косинуса угла
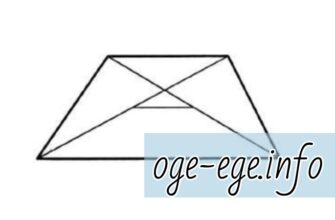
Задача. Основания трапеции равны 29 и 44. Найдите отрезок, соединяющий середины диагоналей трапеции. Решение Средняя линия трапеции проходит
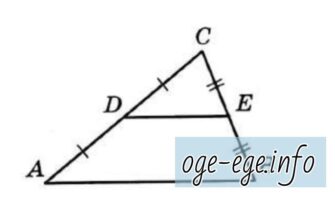
Задача. В треугольнике ABC средняя линия DE параллельна стороне AB. Найдите площадь треугольника ABC, если площадь трапеции ABED равна 36.

Задача. Ваня бросил игральный кубик, и у него выпало больше 2 очков. Петя бросил игральный кубик, и у него выпало меньше 6 очков.
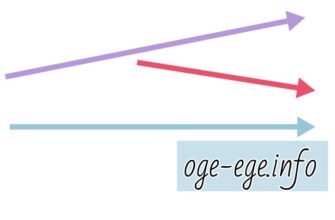
Задача. Даны векторы , и . Найдите , если . Решение Чтобы найти , выполним следующие шаги: 1. Сложим векторы и по компонентам: 2.

Задача. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «

Задача. В ящике 7 красных и 3 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый
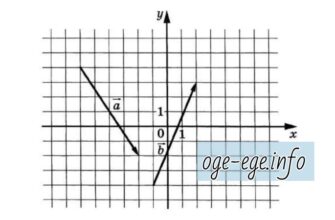
На координатной плоскости изображены векторы и . Найдите скалярное произведение векторов 2 и . Решение Определим координаты векторов

Задача. На одной полке стоит 25 блюдец: 16 красных и 9 синих. На другой полке стоит 25 чашек: 13 красных и 12 синих. Наугад берут два
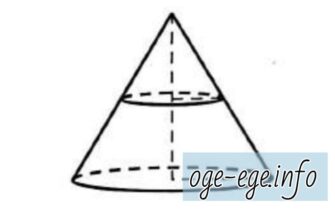
Задача. Площадь полной поверхности конуса равна 66. Параллельно основанию конуса проведено сечение, делящее высоту пополам.