Подготовка к ОГЭ и ЕГЭ - решение заданий и теория
На oge-ege.info, мы предлагаем всестороннюю поддержку для учащихся, готовящихся к ОГЭ и ЕГЭ. Наша миссия - обеспечить вас всеми необходимыми знаниями для успешной сдачи экзаменов.
📚 Что мы предлагаем:
- База заданий: большая коллекция заданий ОГЭ и ЕГЭ с подробными решениями и пояснениями.
- Видеоуроки: наши эксперты предлагают обучающие видео для более глубокого понимания сложных тем.
- Теория и формулы: для безошибочного продвижения вперед.
💡 Почему выбирают нас:
- Актуальность материалов: мы регулярно обновляем нашу базу заданий, чтобы она соответствовала последним требованиям экзаменов.
- Доступность: получите доступ к учебным материалам в любое время, из любой точки мира.
- Пошаговое объяснение решений: все решения подробно объясняются.
🔍 Начните свою подготовку сегодня:
- Изучайте материалы и решайте задания.
- Смотрите видеоуроки и разборы заданий.
📢 Присоединяйтесь к oge-ege.info и сделайте свой путь к успешной сдаче ОГЭ и ЕГЭ проще и эффективнее!
Интересные задания ОГЭ и ЕГЭ (ФИПИ) и их решение
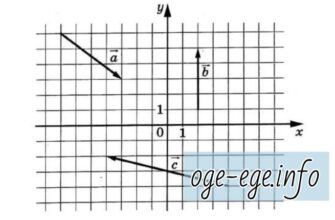
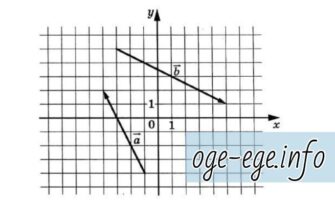
На координатной плоскости изображены векторы , и . Найдите длину вектора . Решение Найдем координаты вектора, для этого найдем координаты

Задача. В коробке 6 синих, 12 красных и 7 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что
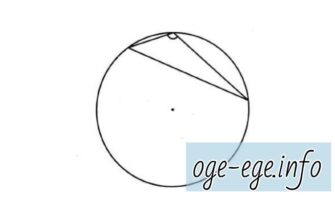
Задача. Радиус окружности равен . Найдите величину тупого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.
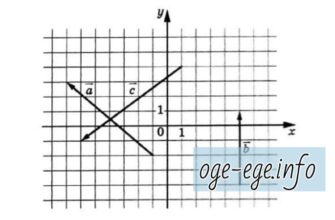
Задача. На координатной плоскости изображены векторы , и . Найдите скалярное произведение . Решение Найдем координаты точек начала и конца
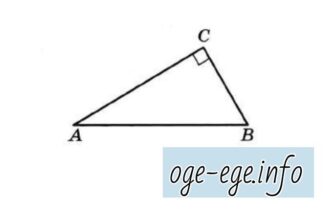
В треугольнике ABC угол С равен 90°, , . Найдите . Решение Запишем соотношение сторон и углов в треугольнике: Чтобы найти AC нам надо знать AB.
Задача. Даны векторы и . Известно, что векторы и сонаправленные, а . Найдите . Решение Для решения этой задачи нужно учесть два условия
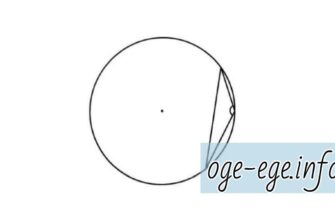
Задача. Найдите хорду, на которую опирается угол 135º, вписанный в окружность радиуса 3\/2. Решение Сделаем рисунок к задаче.
Задача. На координатной плоскости изображены векторы и . Найдите , где — угол между векторами и . Решение Для нахождения косинуса угла
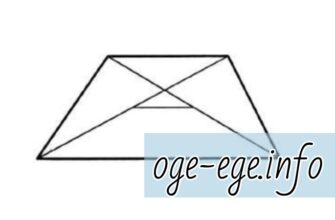
Задача. Основания трапеции равны 29 и 44. Найдите отрезок, соединяющий середины диагоналей трапеции. Решение Средняя линия трапеции проходит

Задача. Ваня бросил игральный кубик, и у него выпало больше 2 очков. Петя бросил игральный кубик, и у него выпало меньше 6 очков.
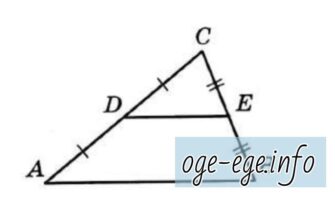
Задача. В треугольнике ABC средняя линия DE параллельна стороне AB. Найдите площадь треугольника ABC, если площадь трапеции ABED равна 36.

Задача. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «

Задача. В ящике 7 красных и 3 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый
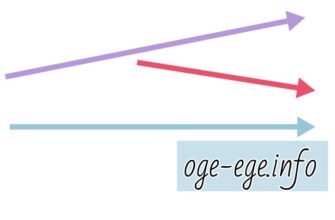
Задача. Даны векторы , и . Найдите , если . Решение Чтобы найти , выполним следующие шаги: 1. Сложим векторы и по компонентам: 2.
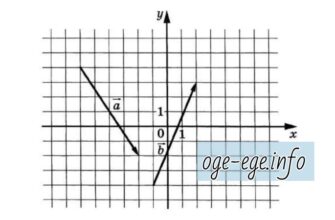
На координатной плоскости изображены векторы и . Найдите скалярное произведение векторов 2 и . Решение Определим координаты векторов

Задача. На одной полке стоит 25 блюдец: 16 красных и 9 синих. На другой полке стоит 25 чашек: 13 красных и 12 синих. Наугад берут два
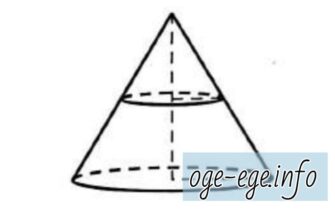
Задача. Площадь полной поверхности конуса равна 66. Параллельно основанию конуса проведено сечение, делящее высоту пополам.