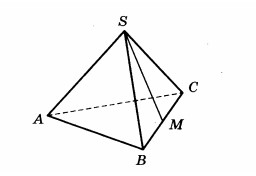
В правильной треугольной пирамиде SABC точка M середина ребра BC S вершина. Известно что SM=5, а площадь боковой поверхности равна 45. Найдите длину отрезка АВ.[latexpage]
Решение: Нарисуем пирамиду и отметим на ней все указанные в условии точки. Так как пирамида правильная — в основании у нее лежит правильный треугольник ABC, все стороны которого равны $AB=BC=AC=a$. Площадь боковой поверхности такой пирамиды — это сумма площадей треугольников SAB, SBC и SAC. Так как основания этих треугольников равны, а вершина пирамиды равноудалена от сторон ее основания, то и сами треугольники равны и являются в правильной пирамиде равнобедренными, то есть мы можем взять любой из треугольников SAB, SBC или SAC, например, удобнее взять треугольник SBC. Так как в нем дана высота SM (M — середина основания равнобедренного треугольника SBC, то есть SM=h — медиана — является также высотой и биссектрисой). Площадь треугольника SBC: $S_{SBC}=\frac{1}{2} \cdot SM \cdot a$.
Боковая поверхность пирамиды равна $S$ бок $=3 \cdot S_{SBC}$ или $S$ бок $=\frac{3}{2} \cdot SM \cdot a$. Так как $S$ бок $=45$, а $SM=5$, получаем уравнение:
$45=\frac{3}{2} \cdot 5\cdot a$
Решаем уравнение:
$9=\frac{3}{2} a$
$a=6$.
Ответ: 6