Радиус основания конуса равен 12, а высота конуса равна 5.
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.
б) Найдите расстояние от плоскости сечения до центра основания конуса.
Решение:
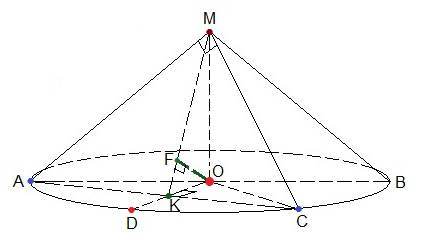
Пусть дан конус с осевым сечением MAB, радиус основания AO=12, высота MO=5.
Найдем образующую конуса. Рассмотрим прямоугольный треугольник АОМ. Катеты AO=12 и MO=5, следовательно, по теореме Пифагора
гипотенуза МА2 = АО2 + МО2 =122 + 52 = 144 + 25 = 169, отсюда МА=13 (запомните эту пифагорову «тройку»: 5; 12; 13).
а) Через вершину конуса М и две образующие MA и MC проходит сечение конуса АMC так, что MA⟘MC. Сечение представляет собой прямоугольный равнобедренный треугольник АМС, который пересекает основание конуса по прямой АС, причем АС — хорда окружности с центром в точке О и радиусом АО, является гипотенузой равнобедренного прямоугольного треугольника АМС, и равна
![]()
б) Найдем расстояние от плоскости АМС до точки О — центра основания конуса. Сделаем дополнительные построения.
Проведем радиус OD⟘AC.
Радиус, перпендикулярный хорде, делит ее пополам.
Точка К – середина АС. Соединим точки М и К. В равнобедренном прямоугольном треугольнике АМС, МК — медиана, а значит, и высота.
Медиана прямоугольного треугольника, проведенная к гипотенузе равна половине гипотенузы.
![]()
Так как МК⟘АС и ОК⟘АС, то плоскость МОК перпендикулярна плоскости АМС, поэтому перпендикуляр, проведенный из точки О к МК будет расстоянием от точки О до плоскости АМС.
В прямоугольном треугольнике МОК мы знаем гипотенузу МК и катет МО.
Найдем второй катет ОК по теореме Пифагора.

Проведем OF⟘MK.
OF- искомый отрезок. OF — высота прямоугольного треугольника МОК, проведенная к гипотенузе МК.
Из подобия прямоугольных треугольников МОК и МFО (по углам) следует:









