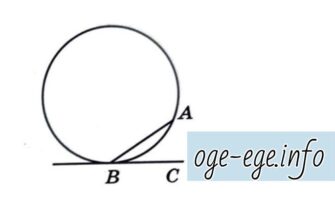Задача. Углы B и C треугольника ABC равны соответственно 13° и 17°. Найдите ВС, если радиус окружности, описанной около треугольника АВС, равен 6.
Решение. Пусть в Δ АВС ∠АВС = 13° и ∠АСВ = 17°, тогда третий угол — ∠ВАС = 180°-(13°+17°) = 150°. Около Δ АВС описана окружность с центром в точке О и радиусом R=ОВ=6. Требуется найти сторону ВС. Вспомним теорему синусов. Стороны любого треугольника пропорциональны синусам противолежащих углов:
Нам понадобится следствие к этой теореме:
и каждое из отношений равно диаметру окружности, описанной около данного треугольника, т.е.
Отсюда BC = 2R ∙ sin150° = 2 ∙ 6 ∙ sin(180°-30°) = 12 ∙ sin30°=12 ∙ 0,5 = 6.
Ответ: 6.
