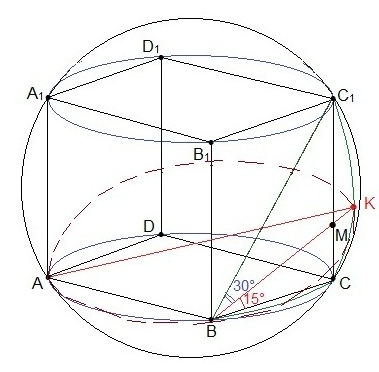
Вокруг куба ABCDA1B1C1D1 с ребром 2 описана сфера. На ребре СС1 взята точка М так, что плоскость, проходящая через точки А, В и М, образует угол 15° с плоскостью АВС.
а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В и М.
б) Найдите длину линии пересечения плоскости АВМ и сферы.

Решение.
Продолжим ВМ до пересечения с поверхностью шара и получим точку К. Плоскость сечения есть круг, описанный около прямоугольного ∆АВК (∠В=900 по ТТП, так как АВ перпендикулярно проекции ВС наклонной ВК и проходит через основание В этой наклонной).
Длина линии пересечения плоскости АВМ и сферы – это длина окрестности, описанной около прямоугольника ∆АВК и равна С=2πR, где 2R=AK. Тогда C=π·AK. Точка К принадлежит плоскости грани BB1C1С. Это точка окружности, описанной около BB1C1С. Диаметр этой окружности BC1. Таким образом, ∆BКC1 – прямоугольный. Так как ∠КВС=150 , то ∠C1BК=450-150=300. BK=BC1·cos300. Если ребро куба равно 2, то
![]()
Из прямоугольного ∆АВК по теореме Пифагора:
![]()
Искомая длина линии пересечения:
![]()