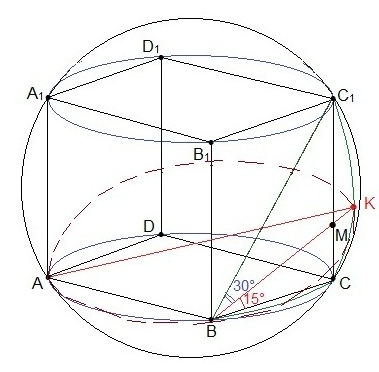
Вокруг куба ABCDA1B1C1D1 с ребром 3 описана сфера. На ребре СС1 взята точка М так, что плоскость, проходящая через точки А, В и М, образует угол 15° с плоскостью АВС.
а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В и М.
б) Найдите длину линии пересечения плоскости сечения и сферы.
 Решение.
Решение.
а) Проведем BM и продолжим до пересечения со сферой. Точку пересечения обозначим через К. Точку К соединим с точкой А и рассмотрим ∆ АВК. По ТТП (теореме о трех перпендикулярах) прямая АВ, проходящая через основание наклонной МВ, перпендикулярно ее проекции ВС, будет перпендикулярна и самой наклонной, т.е. МВ (или КВ) образует с АВ прямой угол.
Всякое сечение сферы плоскостью есть окружность.
Эта окружность будет описана около прямоугольного треугольника АВК, следовательно, гипотенуза этого треугольника будет являться диаметром этой окружности.

б) Длина линии пересечения плоскости сечения и сферы – это длина построенной нами окружности. Диаметр окружности АК. Длину окружности найдем по формуле С = πd, где d = AK.
Точка K лежит в плоскости грани BB1C1C, и если около этой грани описать окружность, пересекающую сферу, то точка К принадлежит и этой окружности и сфере и треугольник ВКС1 – прямоугольный.
∠СВК = 15° по условию, отсюда ∠С1ВК = 45° — 15° = 30°.









